Caso de estudio: Esperanza de vida a nivel global (OMS/WHO)

Durante toda la existencia de la humanidad, las personas se han obsesionado con un único objetivo, vivir más tiempo. Hoy en día, existen miles de estudios sobre los factores determinantes en la cantidad de años que una persona vive y la calidad con la que lo hace. De ese deseo inherente en las personas, es que aparecen datasets como el que vamos a analizar en este caso de estudio. Estos datos fueron tomados directamente de la organización mundial de la salud y poseen datos sobre la esperanza de vida en cada país entre los años 2000 y 2015. Asimismo, muestra datos específicos de estas poblaciones en cada año que, de ser analizada correlacionalmente, nos puede permitir crear modelos y predecir cuanto puede vivir una persona de acuerdo a estos.

Dataset

Como se menciona anteriormente, este dataset tiene datos de todos los paises adheridos a la OMS entre los años 2000 y 2015. Además, para cada uno de esos años y para cada país, contiene los siguientes datos:

Objetivo

Realizaremos un análisis extensivo del dataset utilizando Python con el fin de estudiar y obtener información interesante del dataset. Se recomienda Google Colab para Python por ser gratuito y tener ya instaladas todas las librerías que vamos a necesitar.

Preparación de datos

Como siempre, hay que comenzar analizando y limpiando los datos del dataset. Comenzamos por importar las librerías que vamos a utilizar en el resto del caso de estudio. 

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import scipy.stats as stats
from scipy.stats.mstats import winsorize
from sklearn.decomposition import PCA
from sklearn.preprocessing import scale
import os
%matplotlib inline

Luego, cargamos el dataset utilizando pandas y usamos el método "head" para obtener un primer vistazo a los datos. 

dataset = pd.read_csv('../input/life-expectancy-who/Life Expectancy Data.csv')
dataset.head()

Primero que nada, vamos a utilizar el método "describe" de pandas para obtener una vista estadística de las columnas del dataset: 

dataset.describe().iloc[:, 1:]

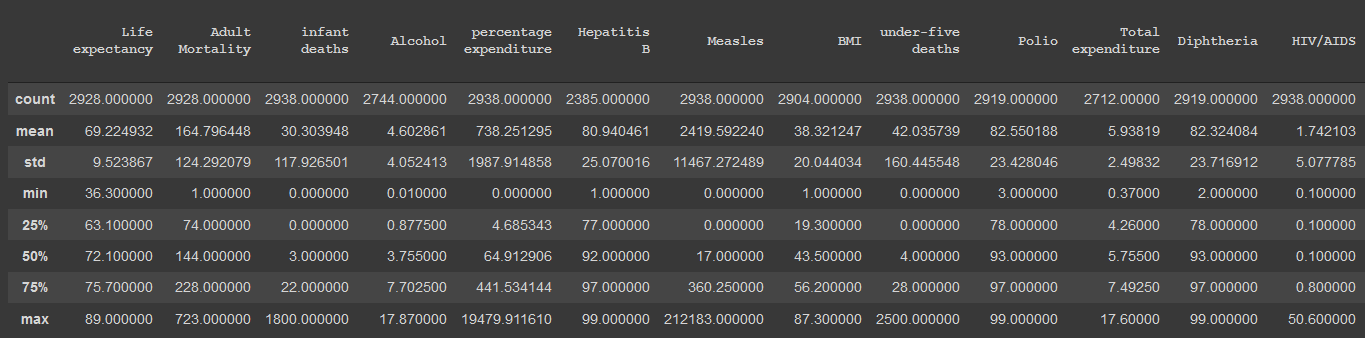
De esta vista, obtenemos datos muy interesantes, principalmente lo siguiente:

Manejo de outliers

Dada esta vista general, es que con un poco de investigación en internet, podemos decidir rangos arbitrarios en los cuales no consideremos datos como outliers.

Ya que los nombres de las columnas vienen todos desestandarizados, es que vamos a quitar todos los espacios en ellos y cambiar aquellos espacios intermedios en los nombres por "_". Luego, aplicaremos funciones lambda marcar los datos que consideramos outliers como outliers (los marcamos como NaN). 

orig_cols = list(dataset.columns)
new_cols = []
for col in orig_cols:
    new_cols.append(col.strip().replace('  ', ' ').replace(' ', '_').lower())
dataset.columns = new_cols

dataset['infant_deaths'] = dataset['infant_deaths'].replace(0, np.nan)
dataset.bmi = dataset.apply(lambda x: np.nan if (x.bmi < 10 or x.bmi > 50) else x.bmi, axis=1)
dataset['gdp'] = dataset.apply(lambda x: np.nan if (x['gdp'] < 200) else x['gdp'], axis=1)
dataset['thinness_1-19_years'] = dataset.apply(lambda x: np.nan if (x['thinness_1-19_years'] < 0.5) else x['thinness_1-19_years'], axis=1)
dataset['thinness_5-9_years'] = dataset.apply(lambda x: np.nan if (x['thinness_5-9_years'] < 0.5) else x['thinness_5-9_years'], axis=1)
dataset['schooling'] = dataset['schooling'].replace(0, np.nan)

Luego, podemos correr la función descriptiva nuevamente para verificar los cambios realizados. Ahora que marcamos aquellos datos outliers como datos faltantes, vamos a hacer una vista general de la cantidad de datos faltantes en el dataset. 

dataset.info()

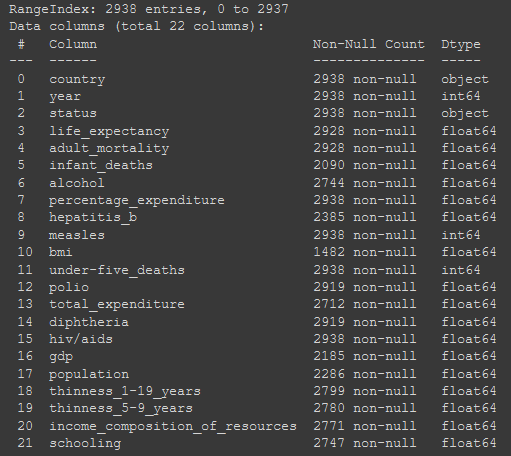
Sabiendo que el total son 2938 datos, vemos como casi todas las columnas tienen menos de 30% de los valores como faltantes, exceptuando bmi, el cual tiene casi un 50% de los valores faltantes. Con este dato, podríamos comprometer el análisis ya que deberemos inferir los valores de la mitad de sus filas en el arreglo de los faltantes, por lo que se toma la decisión de eliminar dicha columna. 

dataset.drop(columns='bmi', inplace=True)

Arreglo de datos faltantes

Para arreglar los datos faltantes, vamos a reemplazar, tanto los que marcamos en el paso anterior como los datos que ya estaban en el dataset con el promedio del resto de los datos para cada columna.

Primero, utilizaremos esta funcionalidad de pandas para ver cuales son los atributos con datos faltantes: 

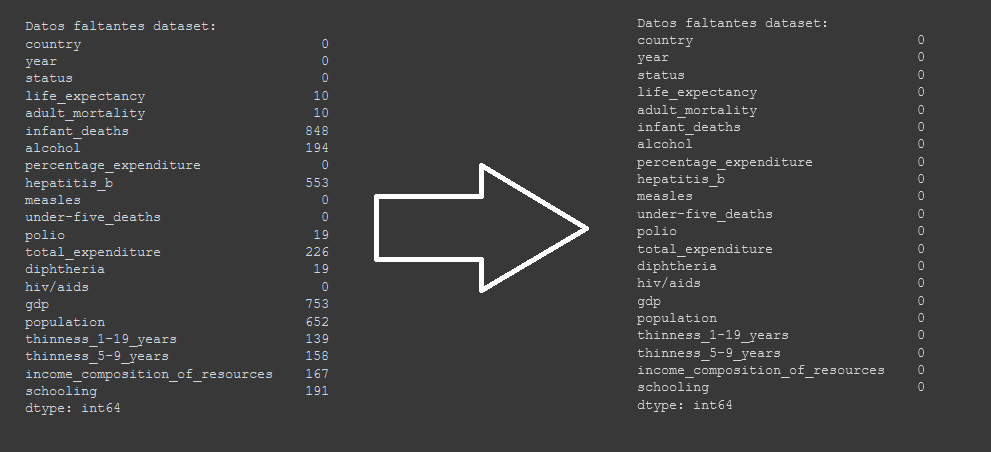
print("Datos faltantes dataset:")
print(pd.isnull(dataset).sum())

De este modo, arreglamos los datos faltantes para cada fila que los tenga. 

dataset["life_expectancy"].fillna(dataset["life_expectancy"].median(), inplace = True)
dataset["adult_mortality"].fillna(dataset["adult_mortality"].median(), inplace = True)
dataset["infant_deaths"].fillna(dataset["infant_deaths"].median(), inplace = True)
dataset["alcohol"].fillna(dataset["alcohol"].median(), inplace = True)
dataset["hepatitis_b"].fillna(dataset["hepatitis_b"].median(), inplace = True)
dataset["polio"].fillna(dataset["polio"].median(), inplace = True)
dataset["total_expenditure"].fillna(dataset["total_expenditure"].median(), inplace = True)
dataset["diphtheria"].fillna(dataset["diphtheria"].median(), inplace = True)
dataset["gdp"].fillna(dataset["gdp"].median(), inplace = True)
dataset["population"].fillna(dataset["population"].median(), inplace = True)
dataset["thinness_1-19_years"].fillna(dataset["thinness_1-19_years"].median(), inplace = True)
dataset["thinness_5-9_years"].fillna(dataset["thinness_5-9_years"].median(), inplace = True)
dataset["income_composition_of_resources"].fillna(dataset["income_composition_of_resources"].median(), inplace = True)
dataset["schooling"].fillna(dataset["schooling"].median(), inplace = True)

Analisis de los datos

Para comenzar este análisis, vamos a graficar lo más importante para visualizar esta data, la esperanza de vida en función de cada uno de los atributos. 

plt.figure(figsize=(15, 20))
for i, col in enumerate(list(dataset.columns)[1:], 1):
    plt.subplot(5, 4, i)
    plt.plot(  dataset_clean[col], dataset_clean['life_expectancy'], 'bo', markersize=1)
    plt.title(col)

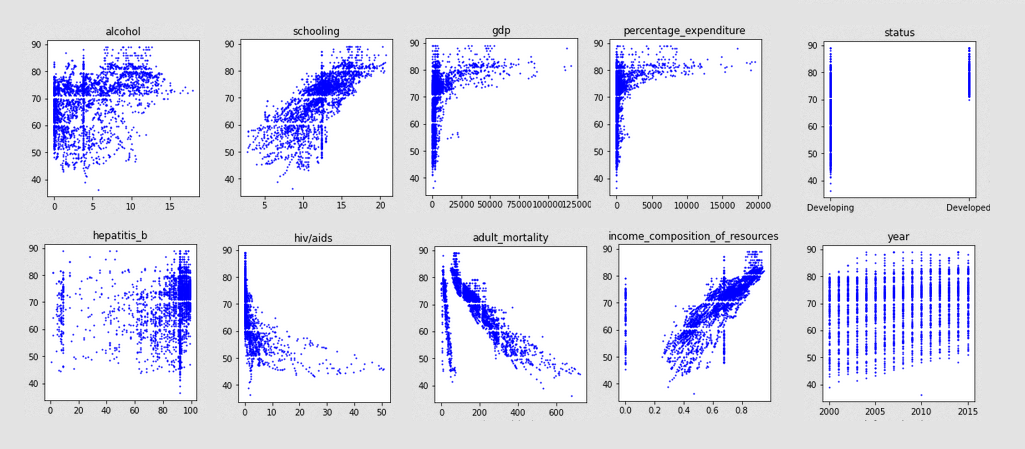
Debido al ruido de los datos, es bastante difícil ver relaciones entre algunos de los datos. Sin embargo otros, muestran tendencias bastante correlacionadas con lo sabido del tema:

De las observaciones anteriores, quizas podríamos generalizar diciendo que los factores que más afectan a la esperanza de vida, son los económicos y los de prevención en salud.
A continuación, crearemos una matriz de correlación para poder sacar mayores conclusiones. 

plt.figure(figsize=(20,15))
sns.heatmap(dataset.corr(), square=True, annot=True, linewidths=.5, cmap="Oranges")
plt.title("Matriz de correlación")
plt.show()

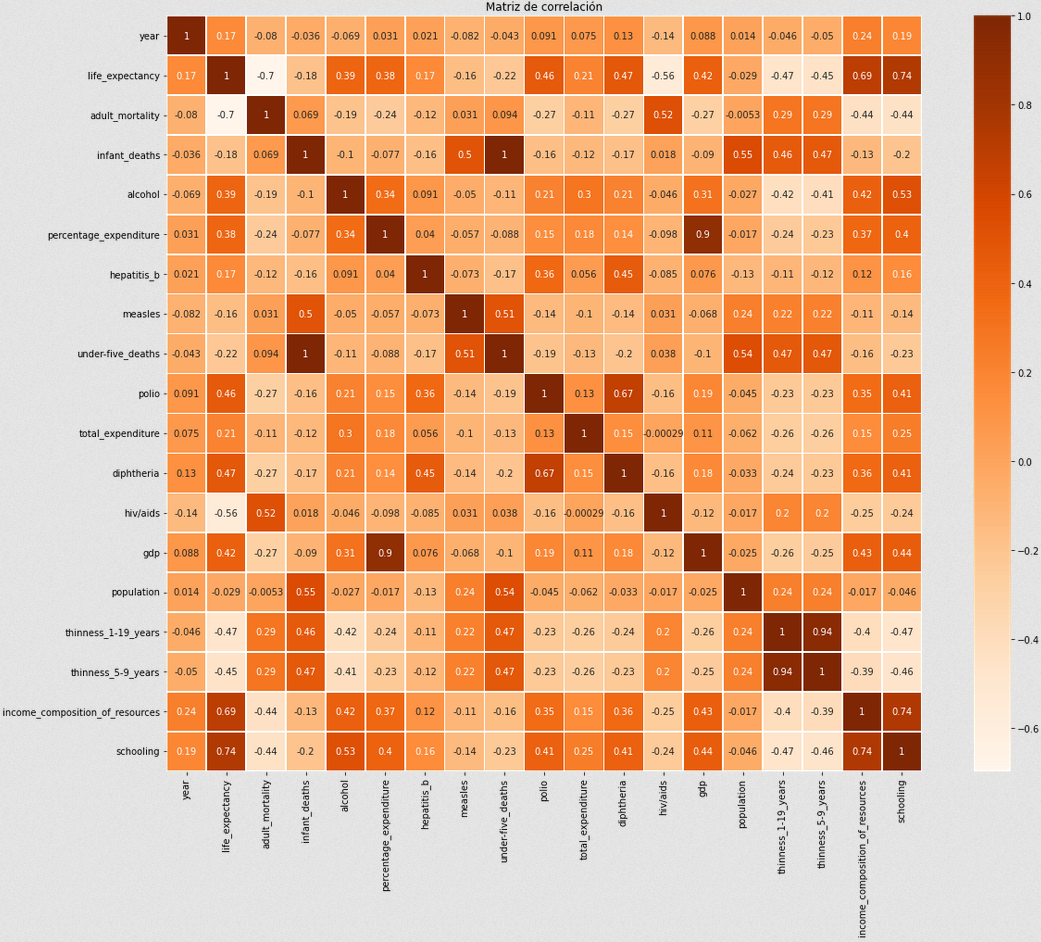
Viendo la segunda columna o la segunda fila, podemos analizar la correlación de los atributos con la salida, life_expectancy. Curiosamente, vemos como los factores con mayor correlación son aquellos relacionados a lo económico y la salud, como habíamos visto antes.

Los que más destacan son:

Además, podemos ver correlaciones inversas (cuando una decrece, la otra crece y viceversa) grandes en los aspectos más relacionados a la muerte:

Finalmente, este dataset trae algunos datos curiosos que van en contra de lo que uno podría concluir en la teoría:

Modelado

Preparación de modelado

Para el modelado, utilizaremos Rapidminer. Primero que nada, exportamos los datos preprocesados en python utilizando la función de Pandas para guardar un dataframe como csv. 

dataset.to_csv("./Life Expectancy Clean.csv")

Luego de tener el CSV, nos vamos a Rapidminer, donde importaremos el CSV como un archivo delimitado por comas. Si ocurre que aparece una columna extra "atr1" conteniendo el número de fila de cada una, lo eliminaremos ya que no nos servirá en nuestro análisis.

Una vez importado el proceso, deberemos realizar algunas modificaciones para preparar el modelado:

Creación de modelos

En este caso de estudio, se opta por el uso de la técnica de ensambles para crear modelos. Esta técnica se presenta como el uso en colaboración de varios modelos distintos que se entrenen con la data de entrada y en conjunto luego, tomen decisiones en base a la clasificacion de la misma.

Crearemos ensambles con tres técnicas distintas:

Al final de este artículo, se encontrará un link al proceso de Rapidminer completo para poder visualizarlo y ajustarlo.

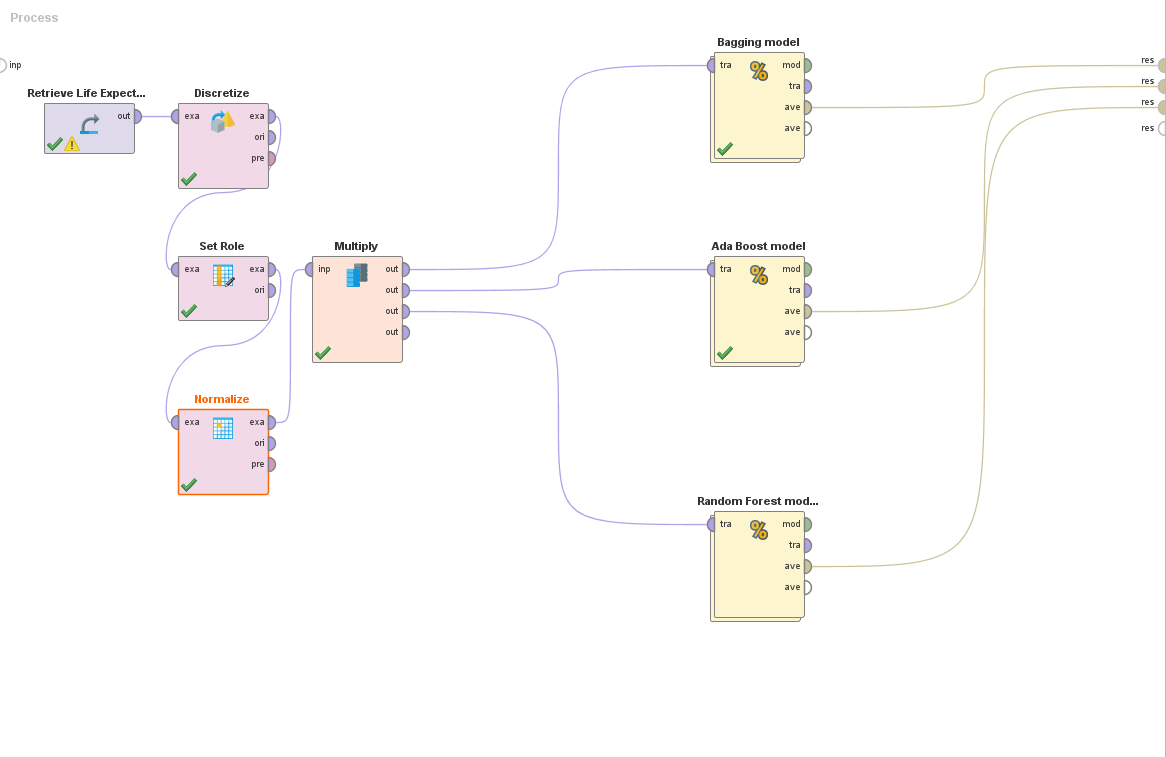
Resultados

Con el fin de estudiar el comportamiento de los algoritmos descritos anteriormente, es que se decide entrenar al modelo con las tres técnicas, en todas, utilizando árboles de decisión.

Se corren Bagging y Boosting con 50 iteraciones cada uno y Random Forest, debido a su naturaleza de no provocar overfitting, con 1000. Todos se corren con la misma semilla de Rapidminer para asegurar que todos tengan las mismas condiciones iniciales.

Resultados Bagging:

Resultados Boosting:

Resultados Random Forest:

Como podemos ver, los resultados indican lo visto en la teoría, Bagging es el que se comporta peor de los tres y Boosting y Random Forest al hacer esas modificaciones randómicas llegan a mucho mayores porcentajes de acierto en el conjunto de test. Asimismo se ve como Random forest tiene un poco más de performance que Bagging, probablemente por el hecho mencionado anteriormente del uso de atributos.

Mejoras

Con el fin de simplificar este modelado, se utilizaron casi todas las opciones por default en todos los bloques de modelado mencionados. Ahora que tenemos el de mejor rendimiento, podemos utilizar el bloque de optimize parameters grid. Esto nos permitirá que Rapidminer cree y pruebe un conjunto acotado de configuraciones del bloque y devuelva aquella configuración con la mayor performance. En este caso, variaremos el número de iteraciones del modelo y el uso de podado en los árboles de decisión (Este proceso es muy pesado en la CPU, dependiendo de cual se usa, puede tardar de minutos a horas).

Resultados Mejora:

Los resultados resultaron ser un poco mejores que el modelo anterior, esto se logró con el uso de 3000 árboles (iteraciones) y sin la utilización de podado. Esto parece indicar que el uso de más árboles mejora la decisión, sin embargo, luego se hace una prueba con 5000 árboles y genera los mismos resultados. Esto quiere decir que en un principio se utilizó pocos árboles y que la cantidad, por lo menos para este dataset y modelo, debe superar los 3000 árboles.

Conclusiones

Referencias