Algoritmos Lineales: Regresión lineal
En Machine learning, existen distintos tipos de algoritmos que permiten crear funciones para poder clasificar datos en distintos tipos. Los algoritmos lineales son aquellos en donde nuestro modelo asume que nuestro conjunto de variables "x" estan linearmente relacionadas con la salida "y", es decir que existe una función f(x) tal que f(x) = a1.x1 + a2.x2 + … + an.xn + b (los pares "ai.xi" corresponden a cada característica que se tenga de los datos).
Regresión lineal simple:
La técnica más clásica de todas, se basa en encontrar una recta: y = ax + b que nos permita a futuro poder determinar datos dada solo una entrada. Las "x" son las variables independientes, es decir, nuestra entrada e "Y" es la salida. La idea es buscar la pendiente "a" y la ordenada "b" para determinar la mejor recta posible de forma que todos los puntos se encuentren lo más cerca de ella como sea posible. Para encontrar la mejor linea de ajuste, se usa habitualmente el método de mínimos cuadrados, técnica de análisis numérico y estadística que busca minimizar la suma de cuadrados de las diferencias en los residuos (las ordenadas b) entre los puntos generados con la función encontrada y los datos.
Regresión lineal múltiple:
Muy parecida a la anterior, salvo que esta permite el uso de más de una entrada "x" de forma de crear una función: f(x) = a1.x1 + a2.x2 + … + an.xn + b. Esto nos permite crear una recta mucho más compleja y más ajustada ya que se usan una mayor cantidad de variables independientes. Algo a tener cuidado con este método es que no siempre es mejor que la simple, ya que usar varias variables independientes donde se tiene una o dos muy correlacionadas con la salida y el resto con poca correlación puede empeorar el rendimiento de nuestro modelo.
Ejemplo en Python:
Para este ejemplo, usaremos un dataset ficticio en el cual definiremos una relación entre las horas de estudio para un examen y la calificación en este.
Importamos las librerías:
import matplotlib.pyplot as plt
from sklearn import linear_model, metrics, model_selection
import numpy as np
import pandas as pd
Cargamos los datos y dibujamos una gráfica para mostrarlos:
num_hours_studied = np.array([1, 3, 3, 4, 5, 6, 7, 7, 8, 8, 10])
exam_score = np.array([18, 26, 31, 40, 55, 62, 71, 70, 75, 85, 97])
plt.scatter(num_hours_studied, exam_score)
plt.xlabel('num_hours_studied')
plt.ylabel('exam_score')
plt.show()
Ahora, utilizaremos le método de regresión lineal de la librería sklearn, dándole como entrada para su entrenamiento los arrays definidos en el paso anterior.
# Entrenar el modelo
exam_model = linear_model.LinearRegression(normalize=True)
x = np.expand_dims(num_hours_studied, 1)
y = exam_score
exam_model.fit(x, y)
a = exam_model.coef_
b = exam_model.intercept_
print(exam_model.coef_)
print(exam_model.intercept_)
De esto obtendremos los valores a y b de la recta y = ax + b. Finalmente, obtendremos una fórmula predictora, y = 9,402x + 4.278. Ahora con esta fórmula podemos predecir valores nuevos simplemente cambiando la x por un valor nuevo de "horas estudiadas".
Para ver los resultados utilizamos el siguiente código para dibujar la recta del paso anterior:
# Ver los resultados
plt.scatter(num_hours_studied, exam_score)
x = np.linspace(0, 10)
y = a*x + b
plt.plot(x, y, 'r')
plt.xlabel('num_hours_studied')
plt.ylabel('exam_score')
plt.show()
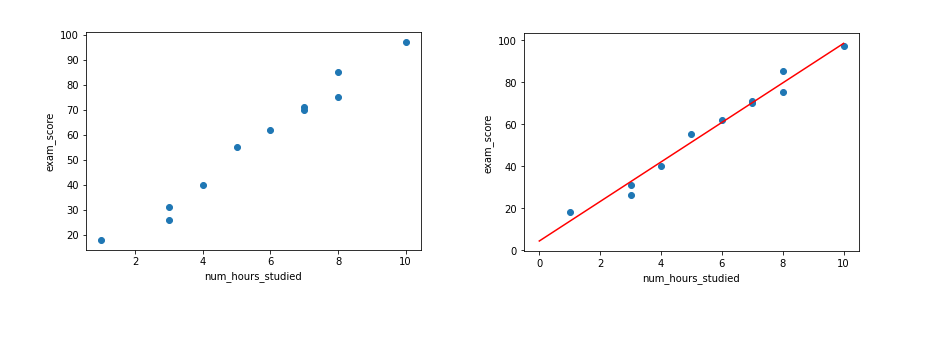
Como podemos ver en estas gráficas, la recta creada se ajusta muy bien a
los datos, eso se basa a que dimos un escenario ficticio en el cual hay
una presunta relación lineal entre las variables, donde a simple vista,
a medida que crecen las horas de estudio, crecen los resultados del
examen.
Algo a tener en cuenta es que estos casos son especiales y no ocurren
muy seguido, por lo que este método no es demasiado aplicable a
problemas más complejos ya que puede haber un gran sobreajuste
(overfitting).